连续域束缚态及其远场观测

作者：于曙超

有观点指出，要判断波是否被完全限制或者束缚在物理系统里面，最简单的方法就是看这个电磁波的频率是否超出了传播波所跨越的连续谱范围，如果超出，则该电磁波就没有辐射到自由空间中的路径或者通道，只能以一种束缚状态的形式存在^[1]。相对的是，若频率包含在连续谱范围内的波的状态是谐振态，并从系统中辐射到无穷远处，则该模式称为泄露模式。

而连续域中的束缚态(Bound States in the Continuums, BICs)是一个例外，它和其他扩展态的波共同存在于连续谱内，却完全被束缚在里面，没有发生任何辐射。BICs广泛存在于各种系统中，与传统的束缚态有着本质的差别。

如图1所示，在某物理系统的连续谱之外，存在传统束缚态的离散能级（绿色线），这种没有向外辐射的通道，如原子核外部轨道上的电子的。在连续谱范围内，会发生类似于束缚态的谐振态（橙色线），该模式存在谐振态和扩展波（蓝色线）的耦合，这类谐振态具有一个被严格定义为出射边界条件的波方程本征值的复合频率ω=ω₀- 𝑖γ，ω₀为谐振频率，γ表示泄露率。连续域中的束缚态中的γ等于0，表示这类谐振态没有泄露出来，完全被束缚在连续谱里面。因此连续中的束缚态可以被认为具有非常窄的谐振线宽和无限大的品质因子，是没有泄露的谐振态，存在谐振态与辐射谱的解耦^[2]。

BICs可以根据其与远场辐射的解耦方式被划分为两大类。一类是对称保护性BICs或可分离式BICs，另外一类是偶发BICs，也被称为调整参数形成的BICs。

对称保护性BICs或可分离式BICs

第一大类可以分为三小类：对称保护性BICs、可分离式BICs和介电常数保护型BICs。

对称保护性BICs

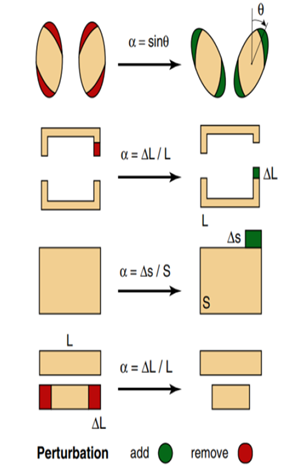
对称保护性BICs的波函数在空间中具有一定的对称性，如旋转对称、镜像对称、轴对称等。只要系统的对称性得以保持，束缚态和扩展态就能保持正交解耦。如果有破坏对称性的扰动，束缚态可能会泄漏到扩展态中，成为准BICs，此时便可以通过实验观测到。

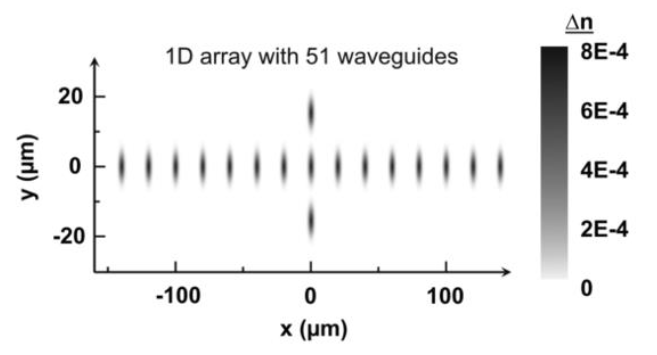
以光波导模型为例，Yonatan Plotnik在2011年提出了一种对称保护型BICs模型^[3]，如图3 所示，两个额外的光波导被分别放置在一维光波导阵列中心波导位置的上方和下方。其中BICs是通过垂直方向上的反对称模式实现的，而所有阵列模式都是对称的。这种结构的BICs不与阵列的任何模式耦合，因此是理想的BICs。通过打破结构对称性，BICs 可以转化为有限寿命的泄漏模式，从而实现光学调控的高效性。

可分离式BICs

介电常数保护型BICs

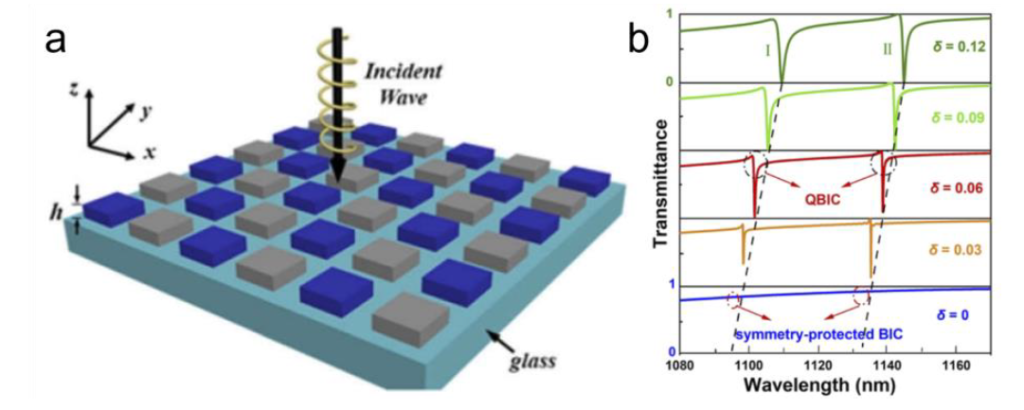
介电常数保护型BICs 是通过在各向同性介电常数中引入不对称性来实现的，这种新的方法允许在保持几何对称的情况下，通过各向同性介电常数的微小变化来操控光学共振^[4]。

偶发性BICs（调参BICs）

第二类也可以分为三小类：Fabry-Perot BICs、Friedrich-Wintgen BICs和单谐振参数BICs。这类BICs可以通过调整系统参数来实现辐射通道之间的干涉相消，从而实现与远场的解耦。

Fabry-Perot BICs

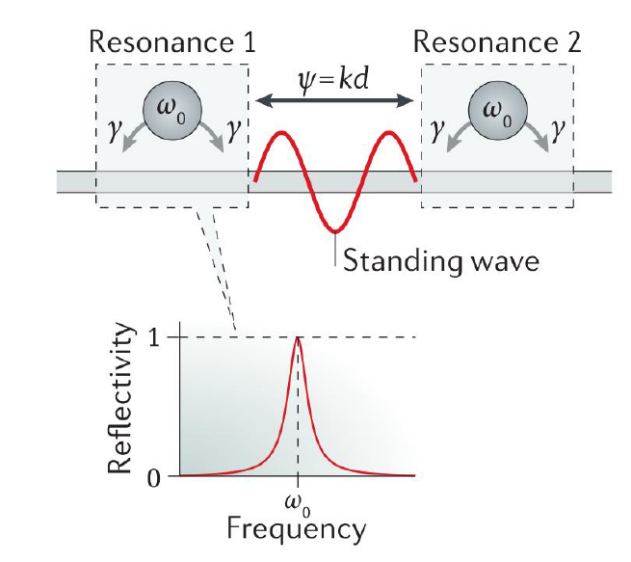
Friedrich-Wintgen BICs

单谐振参数BICs

前面两个激发BICs模式的方法需要两个或多个耦合共振，当参数调谐适当时，单个的谐振也可以激发BICs模式，这个模式被称为单谐振参数BICs模式。

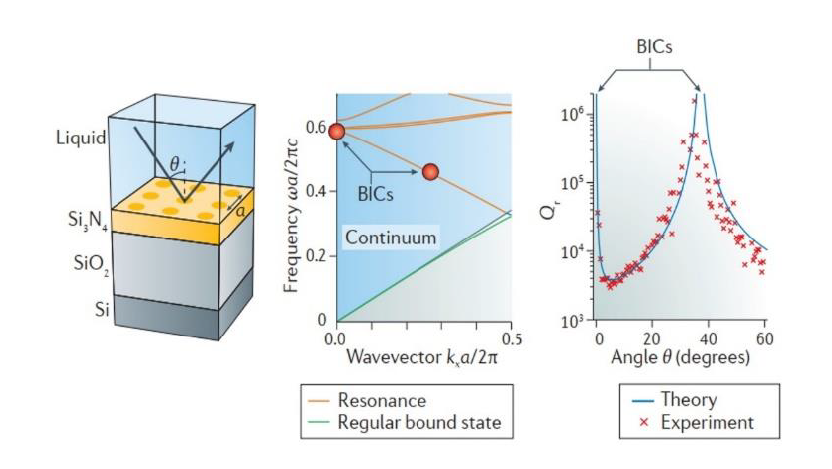
当光子晶体平板具有C2对称性、上下镜像对称和时间反转对称性时，辐射通道的数量就将减少，在沿Γ到X方向的一般k 点处，共振就会转变为束缚态。

从另一个角度来看，这两大类BICs都是通过特定的方式来实现与远场辐射的解耦，但是实现的方法和机制却大不相同。对称保护型BICs依赖于系统的对称性，而偶然BICs则依赖于系统参数的精细调整。这两种方法各有优势，但也有其局限性，需要根据具体的应用场景和需求来选择适合的方法。

因此，理解这两种BICs的工作原理和特性，对于我们设计和实现高效的光子器件和系统至关重要。

太赫兹时域光谱仪（THz-TDS）常用于测量超表面的透射、反射光谱，通常实验中直接得到的是时域信号，需要经过傅里叶变换得到所需的频谱。在实际测量时，由于太赫兹源的信号比较弱，易受外界因素干扰，通常以未加工的空白基底测得的信号为参考，减少基底和探测环境对信号的干扰。在处理数据时，用超表面的透射谱除以参考信号的透射谱，可以得出超表面的传输谱线；在处理相位信息时，则是用超表面的相位谱减去参考基底的相位谱。系统须在干燥环境下进行测量，一般使用空气干燥机或持续通入氮气的方法进行干燥，减少空气中的水分对太赫兹波的吸收。测试中，由于二次反射峰的存在，一般并不能达到极限扫描时长，需要对信号进行截取，但仍可以满足大多数超表面光谱的测试需求^[8]。

参考文献：

[1] Von Neumann J, Wigner E P. Über das Verhalten von Eigenwerten bei adiabatischen Prozessen[M]//Wightman A S. The Collected Works of Eugene Paul Wigner. Berlin, Heidelberg: Springer Berlin Heidelberg, 1993: 294-297.

[2]杨秋生.基于连续域束缚态的全介质非线性超表面研究[D].哈尔滨工程大学,2021.DOI:10.27060/d.cnki.ghbcu.2021.000416.

[3] Plotnik Y, Peleg O, Dreisow F, et al. Experimental Observation of Optical Bound States in the Continuum[J]. Physical Review Letters, 2011, 107(18): 183901.

[4] Yu S, Wang Y, Gao Z, et al. Dual-band polarization-insensitive toroidal dipole quasi-bound states in the continuum in a permittivity-asymmetric all-dielectric meta-surface[J]. Optics Express, 2022, 30(3): 4084-4095.

[5]张星源.基于金属材料的太赫兹超表面结构连续域束缚态的研究[D].天津大学,2022.DOI:10.27356/d.cnki.gtjdu.2022.001358.

[6] Hsu C W, Zhen B, Lee J, et al. Observation of trapped light within the radiation continuum[J]. Nature, 2013, 499(7457): 188-191.

[7]曾德辉.太赫兹幅度调制和相位调制器件研究[D].桂林电子科技大学,2022.DOI:10.27049/d.cnki.ggldc.2022.000312.

[8]陈云.基于耦合模理论的连续域中束缚态超表面器件及耦合应用研究[D].桂林电子科技大学,2024.DOI:10.27049/d.cnki.ggldc.2024.000003.