s-SNOM：定量表征激子--等离子体极化激元强耦合的工具

作者：张启宇

背景：

极化激元是光与物质中的粒子或准粒子发生强相互作用而形成的一种集体振荡模式。散射式扫描近场光学显微镜（s-SNOM）能够对极化激元直接进行实空间成像，这一优势使得学者能够对其进行定量的近场表征，帮助人们对各种类型的极化激元及其相互作用有了更为全面和深刻的研究。然而，目前大多数研究都集中在中红外频段激元的近场定量表征，可见光-近红外范围内的研究工作较少。

近日，Laura N. Casses等人基于反射配置的s-SNOM，在室温下对 WSe2/Au中的激子-等离子体激元（EPPs）进行定量表征。由s-SNOM测得的近场结果可直接获得其Rabi分裂能为81 meV，极化损耗为55 meV，证实该系统处于强耦合模式，此结果与理论预测和远场结果高度一致。该工作发表在ACS photonics期刊（https://doi.org/10.1021/acsphotonics.4c00580）。

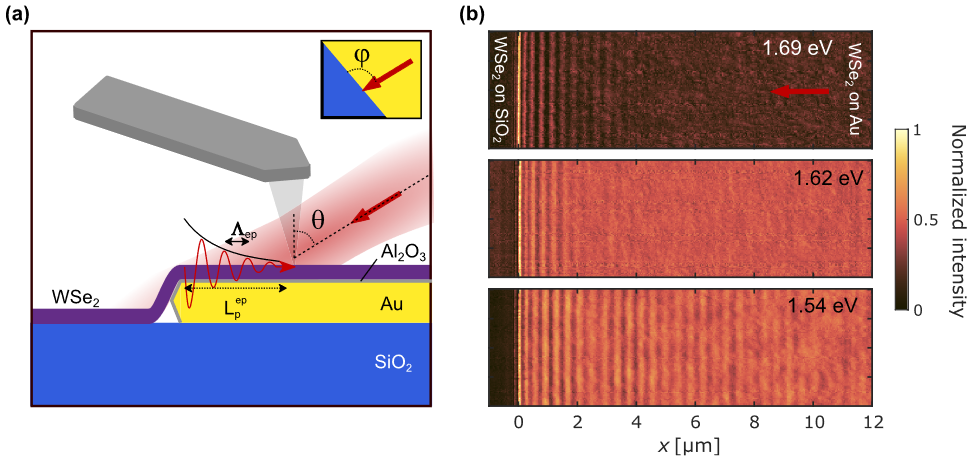
图 1 激子-等离子体激元(EPPs)在单晶金片状WSe2上传播的近场测量。

(a) 实验示意图，其中，Λep为边缘发射光子的波长，Lepp为边缘发射光子的传播长度，θ为偏振入射角。右上角插图展示了样品的俯视图，φ为入射光与样品边缘的夹角；

(b) 三种不同激发能量下的近场强度，x轴的原点位于金板的边缘，箭头代表入射光的方向。

正文：

该工作的结构如图1a所示，13 nm的WSe2被放置在100 nm单晶金盘上并覆盖一个边界，WSe2与Au之间置有2 nm的Al2O3层，激发波长为1.5-1.7 eV。

近场配置下，极化激元的激发方式主要有三种：尖端激发（tip-launched）、边缘激发（edge-launched）和尖端反射边缘激发（tip-reflection edge-launched），多种可能的激励路径导致复杂的干涉模式，使测量分析复杂化。因此，该工作中通过控制入射光与Au盘边缘垂直来使边缘激发比重达到最大，以降低后续分析难度。值得一提的是，该工作刻意将光斑弱聚焦化（直径~50um），使得在扫描过程中边缘始终被入射光覆盖。图1b近场成像图中的干涉条纹展现了EPPs的传播特性，在不同的激发能量下，EPPs的周期和传播距离各有不同。

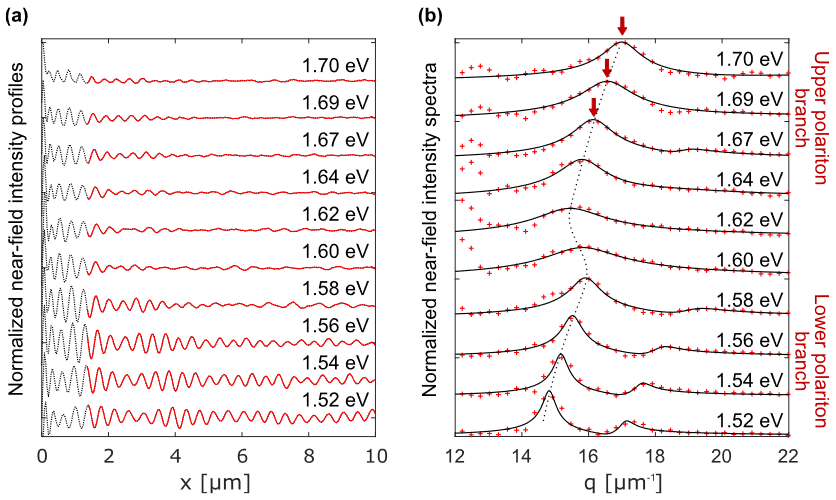
图 2 (a) 基于s-SNOM测量了不同激发能下WSe2 /Al2O3 /Au结构的条纹轮廓，这些剖面的红色部分用于傅里叶变换；

(b) 条纹轮廓的傅里叶变换(红叉)及其拟合(黑色曲线)，红色箭头标识的峰代表边缘发射极化子波矢量Kel的位置。

通过提取垂直于边缘的实空间线轮廓（图2a）并作FFT（图2b），可以直接得到边缘激发EPPs的波矢量值Kel和传播距离Lpep。当针尖靠近边缘时，多种激发方式混合存在，对结果分析产生一定干扰，因此在FFT前截去了距离边缘1.4 um以内的线轮廓。WSe2的A激子能量在1.63 eV附近，图2b中由Kep峰值构成的黑色虚线在1.6 eV附近表现出明显的“反向弯曲”现象，这是激子极化激元的标志特征。

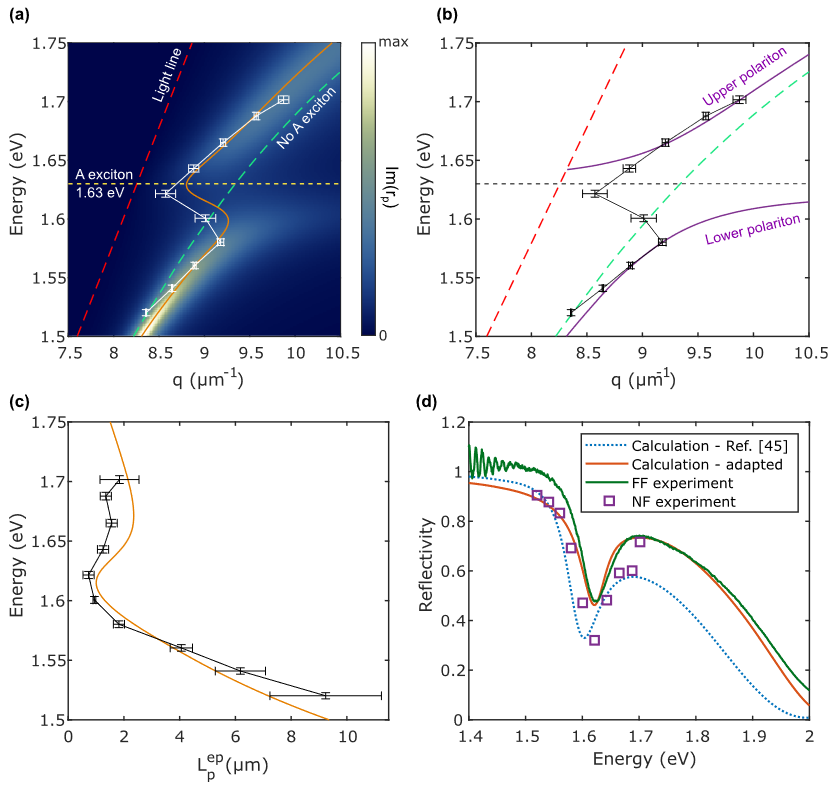
图 3 (a) 13 nm WSe2 /Au的EPPs色散，彩色图显示用TMM计算的反射系数的虚部，带误差条的白线对应于从数据中提取的实验波向量。橙色线表示使用TMM计算的理论色散关系。其中虚线表示空气中的光线，水平虚线表示WSe2的A激子的能量，蓝线表示没有A激子的样品的色散;

(b) 与耦合振荡器模型(COM)的色散关系进行了比较，两个极化子分支用紫色表示，实验波矢量用黑色表示。

(c) 实验(黑色曲线)和理论(橙色曲线)极化子的传播长度。水平误差条对应于拟合的不确定性；

(d) 13 nm WSe2 /Au的反射率比较。使用Munkhbat etal的WSe2介电函数计算(蓝虚线)，直接用传统的远场显微镜测量(绿线)，使用适合远场反射率的电函数计算(红线)，并从近场测量(紫色方块)中提取。

图3a中的白线为实验提取的色散曲线，水平误差棒代表FFT的峰值线宽，竖直误差棒代表激光能量的线宽。为了将实验结果与理论结果进行比较，该工作采用了适用于非各向异性材料的转移矩阵法(TMM)，分别使用两种方法计算出色散曲线。第一种方法是基于该复杂结构的反射系数rp，其极点处的解是一个复数波矢，不同能量下的复波矢实部构成色散曲线（图3a中的橙线）；另一种解则是直接根据rp的虚部绘制色散图（图3a中的背景彩图），这种方法通常与光学态密度（DOS）相关。两种理论计算方法都给出了一致的结果，并与实验结果保持一致。

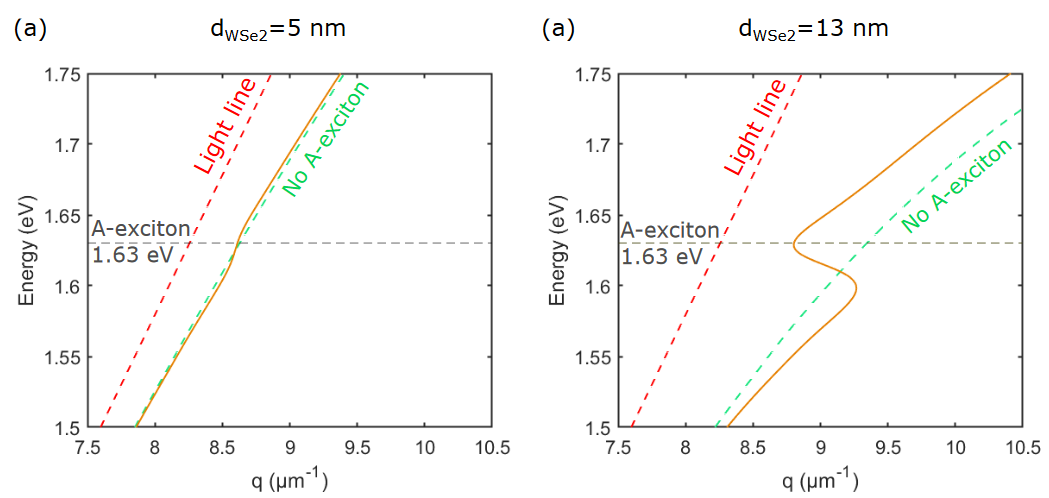
图 4 用TMM计算(a) 5nm厚WSe2和(b) 13nm厚WSe2的激子-等离激元极化的色散关系。橙色的线对应于用TMM计算的理论色散关系。红色虚线表示空气中的光线，水平虚线表示WSe2中A 激子的能量，绿色虚线表示没有A 激子的样品色散。

Rabi分裂能是衡量耦合强度的关键指标。为了预测ERabi，需要首先考虑零失谐状态下的上下分支差异。零失谐状态是在不耦合A激子时WSe2的激子模式与Au的表面等离激元模式的交集，理论计算结构如图3a中的黄色（激子模式）和蓝色（等离激元模式）虚线所示。DOS方法计算出零调谐时(q=9.4 um-1)的ERabi=89 meV，但这种方法计算出的结果往往只能与实验结果作定性的比较，且在该工作中，理论与实验得到的反向弯曲中心有着明显的漂移，这表明在介电函数上直接移除A激子的局限性。此外，该工作还研究了样品厚度对这种方法的剧烈影响（图4）。因此，想要直接通过理论计算得到实际的Rabi分裂能是十分困难的，而通过实验来定量测量ERabi变得更加有意义。

在反向弯曲中心(q=9.0 um-1)，理论计算的ERabi=77 meV，而由实验数据点拟合优化后得到的ERabi=81 meV，二者误差在10%以内，证实了s-SNOM具有定量测ERabi的能力，并且结果具有可靠性。此外，由图3c中的Lpep拟合可以得到EPPs的极化损耗Γ=55 meV。最后，根据公式(1)可以确定复波矢 。

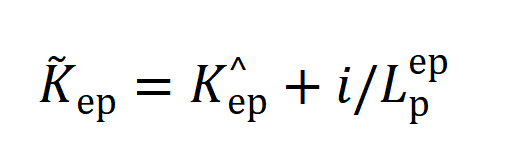
（1）

总结：

基于反射配置的s-SNOM系统，该工作测量了A激子能量附近WSe2/Au多层结构的EPPs。仅利用实验数据，作者得到分裂能ERabi = 81 meV和极化损耗Γ = 55 meV，进而确定了复波矢 ，理论计算和远场实验的结果均证实了结果的可靠性。该工作的方法被预测可以应用于s-SNOM反射配置中不同极化类型的复值波的定量表征，对于设计新的极化器件、理解强耦合状态下的材料特性以及设计新的超表面都具有重要意义。

参考文献：

[1] Casses L N, Zhou B, Lin Q, et al. Full Quantitative Near-Field Characterization of Strongly Coupled Exciton–Plasmon Polaritons in Thin-Layered WSe2 on a Monocrystalline Gold Platelet[J]. ACS Photonics, 2024.